Modelling of Gibbs Energy using Cluster Variation Method(CVM)

Gibbs Energy

The Gibbs energy can be expressed as the sum of a reference term, a mixing term, and a physical model, such as one accounting for magnetic transitions. The mixing term itself comprises an ideal mixing component and an excess term. Different models vary in their treatment of the excess term.

In the first category of models, the excess Gibbs energy of mixing is represented as a polynomial function of composition. These empirical models do not explicitly incorporate short-range order (SRO). In contrast, the second category of models derives the excess Gibbs energy of mixing from statistical mechanics, explicitly accounting for SRO.

The Cluster Variation Method (CVM) belongs to the second group. As a mean-field approach, CVM provides a hierarchy of solutions to the Ising model, offering a reasonably accurate treatment of SRO by considering correlations between neighboring sites.

Modified CVM

The truncation error in the Cluster Variation Method (CVM) entropy functional can be significantly reduced by modifying the multiplicity of the basic cluster term in the entropy functional. This modification is determined by equating the consolute temperature to a more accurate value. This approach improves estimates of enthalpy, entropy, consolute temperature, and short-range order (SRO) without additional computational cost, making it a practical standard for CVM entropy functionals. We have applied this methodology for bcc and fcc structures.

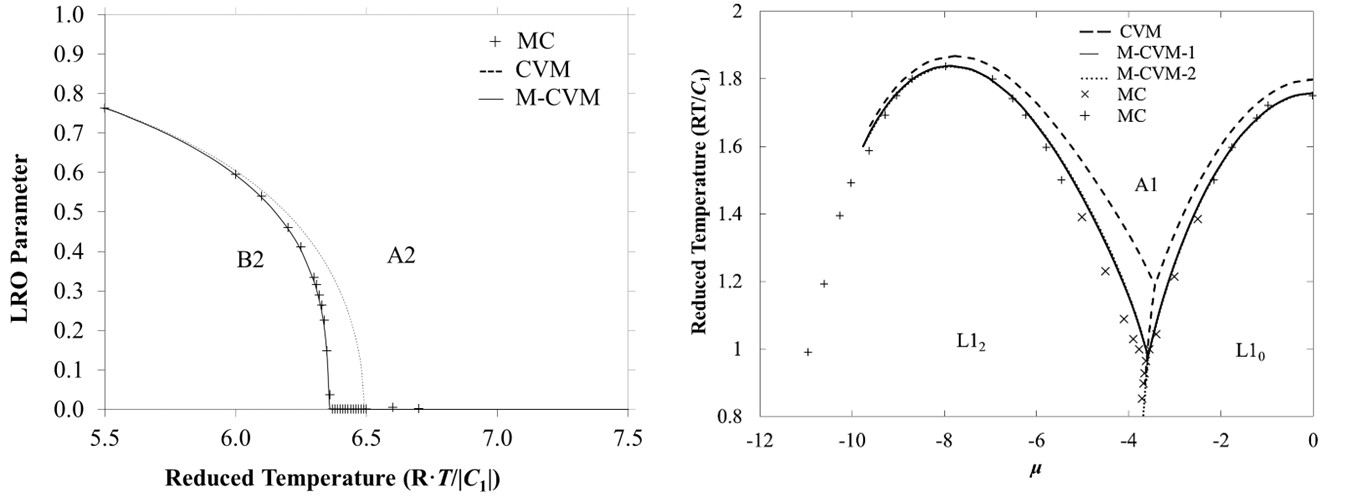
Figure 2: Results for bcc and fcc structures.

Polynomial approximation of correlation function

Correlation Functions (CFs) are typically derived by solving nonlinear equilibrium equations, a process that demands compute-intensive numerical methods. To simplify this, CFs can instead be expressed as polynomial functions of composition, bypassing the need for equilibrium equations. In this approach, the coefficients of the polynomial are rational functions of temperature and energy parameters. This method offers ease of application comparable to CALPHAD techniques while retaining detailed information about short-range order (SRO). It has been successfully applied to the A2–B32 system using the tetrahedron approximation.

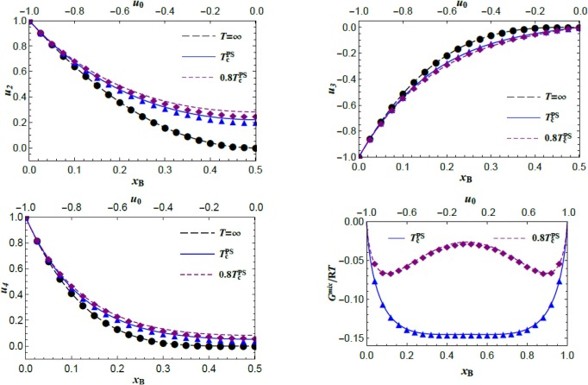
Figure 2: Comparison of CVM and polynomial data for phase separating tendency of A2 phase at various temperatures for (i) II-n pair CF (𝑢2), (ii) triangle CF (𝑢3), (iii) tetrahedron CF (𝑢4) and (iv) Gibbs energy of mixing (𝐺𝑚𝑖𝑥/RT).

Invariant Basis for Multicomponent Systems

Cluster Effective Coefficients (CECs) are not unique and exhibit basis dependence when extended from binary to multicomponent alloys. Unlike CALPHAD methods, CECs lack standardization, making database development challenging. To address this issue, a new framework has been developed that employs configurational variables and corresponding CECs independent of the choice of basis. This framework has been validated for disordered bcc, fcc, and hcp structures, providing a standardized and reliable approach for handling CECs in complex alloy systems.