Theoretical Data

Data

Thermodynamic modeling requires thermochemical and phase equilibrium data. However, experimental data is often limited due to high costs and the challenges of studying non-stable phases, especially when developing new materials. Experimental data is even more limited for multicomponent systems. In such cases, first-principles calculations, particularly those based on density functional theory (DFT), provide a reliable alternative for predicting thermodynamic properties like enthalpy and entropy as functions of temperature, volume, and pressure.

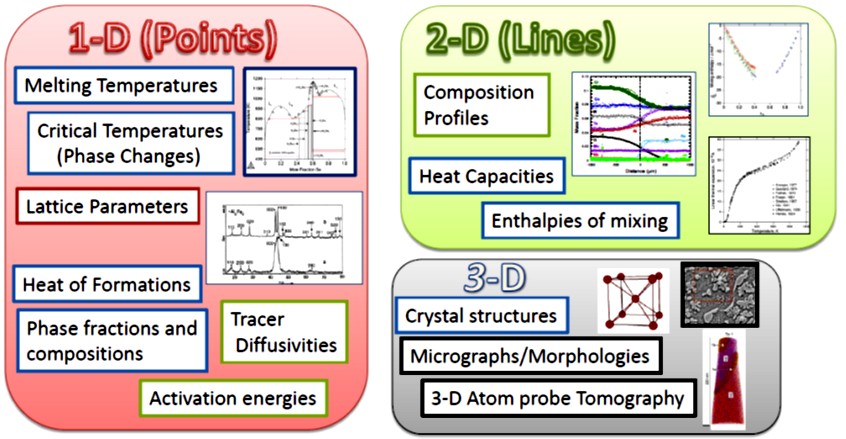
Figure 1: Types of data used for optimization

Thermochemical data, essential for modeling individual phases, is typically harder to obtain experimentally compared to phase equilibrium data, which involves multiple phases and is more accessible. First-principles calculations play a vital role in bridging this gap, providing much-needed thermochemical data to support CALPHAD modeling. This synergy has proven particularly valuable for accurately describing binary and ternary systems and advancing the modeling of complex materials systems.

Ordered Structure

Calculating the energy of an ordered structure using Density Functional Theory (DFT) is straightforward and involves several well-defined steps. First, the crystal structure must be defined, including atomic positions, lattice parameters, and symmetry. Input files are prepared based on the DFT software being used, such as VASP, Quantum ESPRESSO, or CASTEP, and appropriate pseudopotentials (e.g., PAW or USPP) are chosen for the elements in the system. Key computational parameters are then set, including the exchange-correlation functional (commonly PBE within GGA or LDA), a k-point mesh for Brillouin zone integration (e.g., Monkhorst-Pack grid), and a plane-wave energy cutoff that is typically 1.3–1.5 times the maximum recommended value in the pseudopotential file. Convergence criteria for energy and forces are also defined.

Disordered Structure

Calculating the energy of a disordered structure using Density Functional Theory (DFT) involves additional considerations compared to ordered structures, as disorder introduces complexity in representing atomic arrangements and averaging over configurations. At present, there are three main approaches to calculating disordered solution phases: the coherent potential approximation (CPA)) (Sigli et al. 1986), the cluster expansion (CE) (Wolverton & Zunger 1995), and the special quasirandom structures (SQS)) (Wei et al. 1990) (Zunger et al. 1990) approach (Z.-K. Liu and Wang 2016).

SQS (Special Quasirandom Structures)

SQS represents the best periodic supercell approximation to the true disordered state for a given number of atoms per supercell (Zunger et al. 1990). SQS is optimal according to the criterion that a specified set of correlations between neighboring site occupations in the SQS match the corresponding correlation of the true, fully disordered state. The SQS’s for fcc-based alloys and bcc alloys have been generated by Wei et al. (Wei et al. 1990) and Jiang et al. (Jiang et al. 2004), respectively.

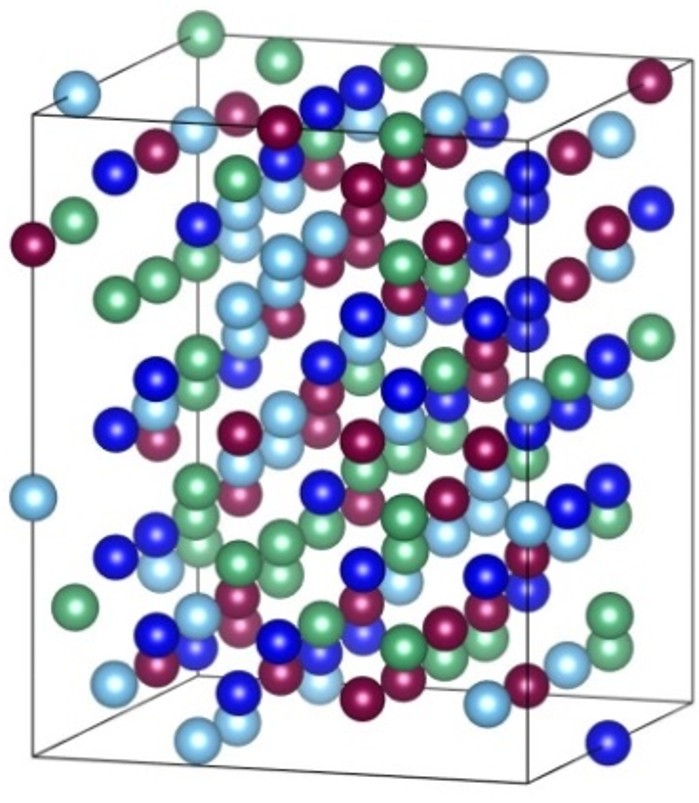
Figure 2: SQS Structure for bcc Mo-Nb-Ti-W Alloy Systems

Cluster Expansion (CE)

The cluster expansion method, introduced by Sanchez, Ducastelle, and Gratias (1984), is widely used to model configurational properties by describing the energy in terms of correlation functions and effective cluster interactions (ECIs). This method provides a computationally efficient way to capture the energetics of disordered systems, especially when combined with Monte Carlo simulations.

Any function of configuration such as the configurational enthalpy H_c for a binary phase can be expressed as a bilinear sum of the products of the correlation functions and their respective cluster expansion coefficients (CECs). This idea is very analogous to a Taylor or Fourier expansion. The function \( H_c \) can be expressed as (J. M. M. Sanchez, Ducastelle, and Gratias 1984; J. M. Sanchez 2010).

The equation for configurational enthalpy \( H_c \) is given by: \[ H_c = \sum_{j=1}^{r_N} C_j m_j u_j \]

Here, the subscript j is an index that serves to identify each distinct cluster type \(r_N\) is the number of all distinct cluster types, \(C_j\) are the CECs and \(m_j\), the multiplicities corresponding to the respective correlation functions \(u_j\). The multiplicities \(m_j\) are defined as the number of symmetry-equivalent clusters of type j per site present in the structure.

The expansion coefficients \(C_j\) are also called effective cluster interactions (ECI’s), and finding their values is the central task when constructing a cluster expansion. A good cluster expansion code aims to find the relevant clusters robustly. In principle, the summation extends from the empty cluster containing no sites to the cluster containing all N atomic sites in the system. In practice, the CECs are expected to be negligible beyond a reasonably small neighborhood.

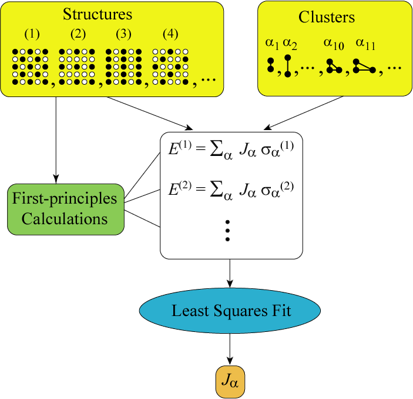
Figure 3: Cluster Expansion Method

Cluster expansion method has been applied fo the Nb-V system.

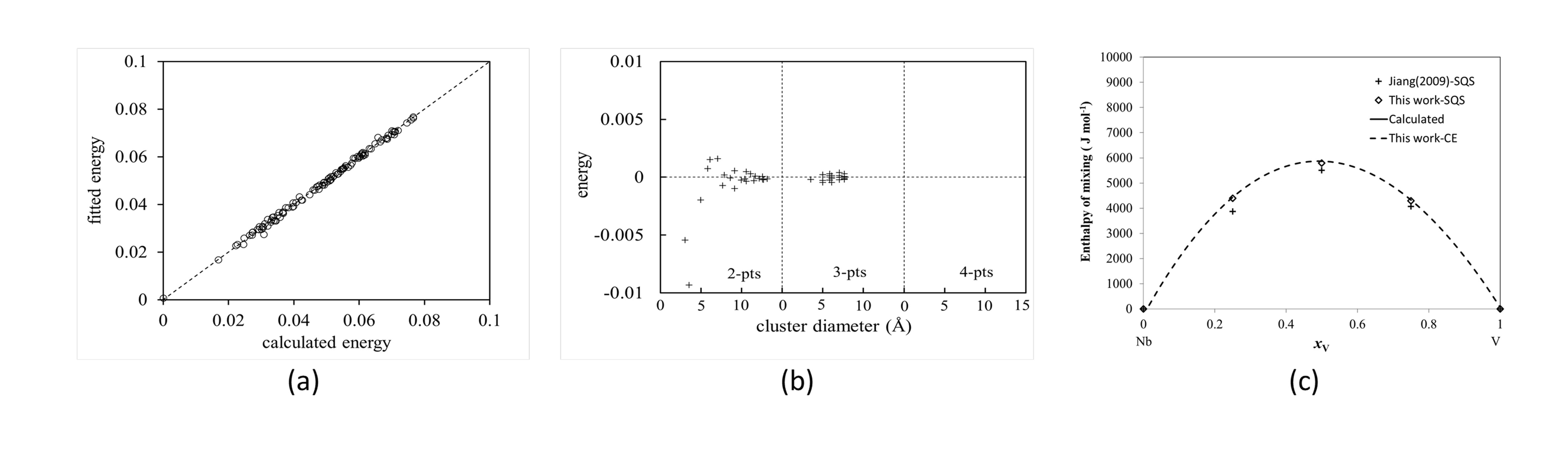
Figure 4: (a) Fitted and calculated energy comparison of Nb-V bcc phase, (b) Variation of ECI vs cluster diameter, (c) Variation of energy with composition.

We have applied CE and SQS for ternary and quaternary systems as well.

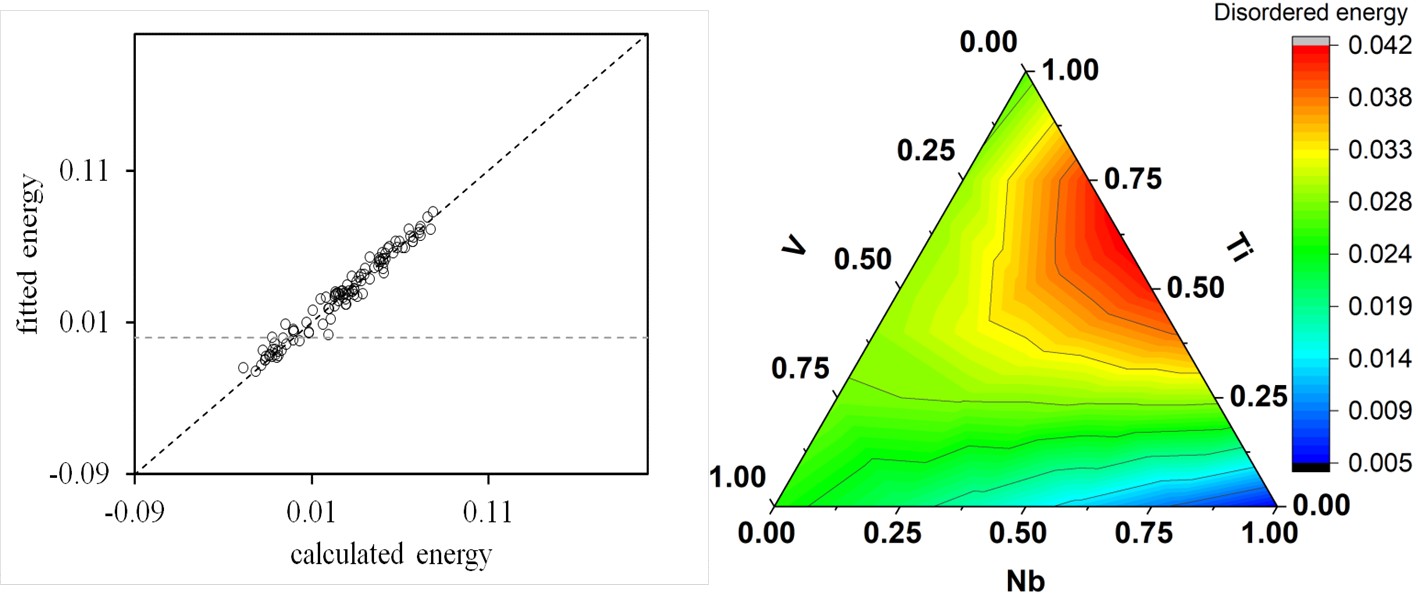
Figure 5: (a) Comparison of enthalpies of formation (eV/atom) obtained from DFT calculations and predicted with CE method of Nb-Ti-V bcc phase (b) energy contour plots

Application of Machine Learning

Cluster expansion (CE) is commonly used to study the relationship between the enthalpy of mixing and correlation functions or short-range order (SRO) parameters. However, CE must be truncated at a certain cluster size, leading to truncation errors. As an alternative, a neural network is trained to model this relationship for the binary subsystems of the NbTiVZr high-entropy alloy (HEA). The training involves generating a large set of structures and their corresponding correlation functions (SRO parameters) using the Alloy Theoretic Automated Toolkit (ATAT), followed by first-principles calculations to determine the enthalpy of mixing. The trained neural network produces predictions that are more accurate than the CE model, offering a clearer understanding of the complex relationship between the enthalpy of mixing and SRO.

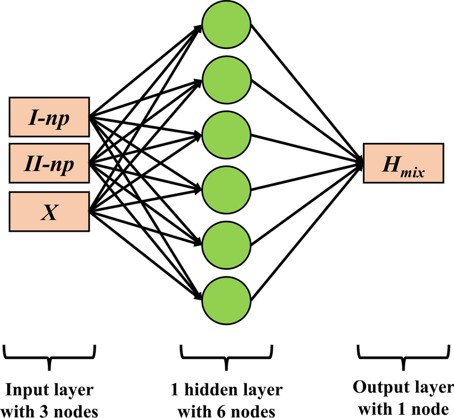
Figure 6: Neural Network Model for Enthalpy Prediction